
Intro
Welcome to the new entry on our series oriented around ML in video game use cases. The entry forms a part of a loosely connected series, the first of which sets up an overview of the problem space, the rationale, and the rough outline of how we’ll proceed. You can read it here if you want – but if you don’t, here’s a tl;dr:
-
we’re concerning ourselves with creating a situation-awareness-improving tool for a sci-fi, simulator-styled, multiplayer, First-Person Shooter, i.e., MechWarrior Online (MWO);
-
our task for now is to identify the position of the target designator on a frame (if present), and extract the image of the target contained within;
-
we’ll use this capability to extract training data (images of targets) to train our "final" model, which will serve as a tool for reviewing gameplay footage, for the purpose of improving situational awareness of players.
As a refresher, the following animation shows what the target designator looks like in the game (marked as 3.):
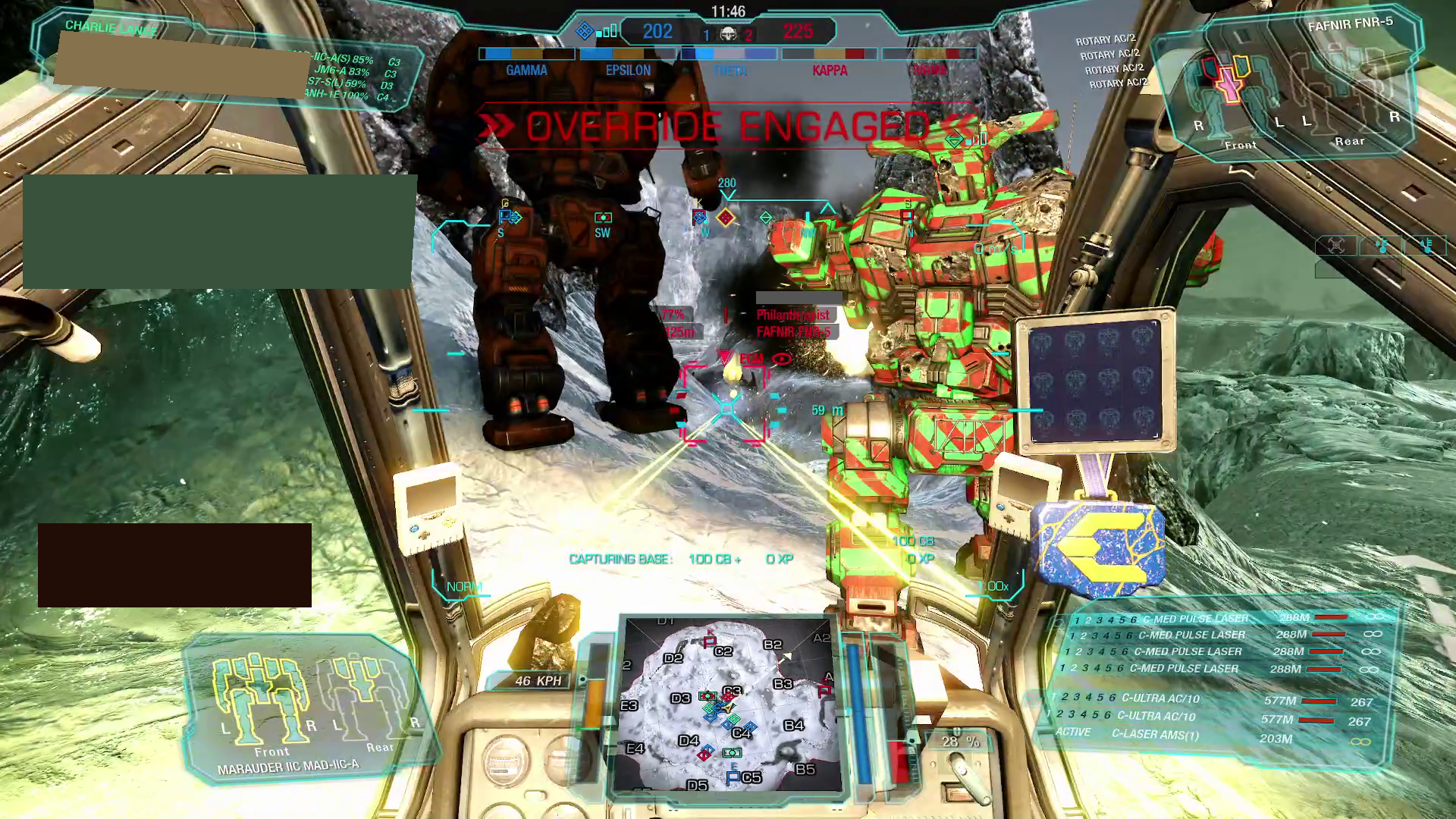
and, in contrast, an example of an "actual", in-match screenshot:
Our general process for the series can be broken down as follows:
-
we’ll first examine a number of different methods for extracting the designator’s position, including hyperparameter optimization, if applicable;
-
after that, we’ll run those methods on a larger dataset, comparing both their efficacy and efficiency.
Somewhere between 1 and 2, we’ll also need to develop a quality measure for extracted images, to minimize the amount of bogus or low-quality training data, such as one in the screenshot below.
However, in this particular blog entry, we’ll focus on Point 0, namely: what makes a target designator in MWO? We’ll explore this question with the use of some basic Data Science methods.
Getting started
We’ll mostly be using OpenCV for frame loading and manipulation, as well as numpy for numeric operations on the frame’s data. Scikit-learn and other (deep) learning frameworks will come into play later.
This post assumes basic knowledge of all of the above (if you’d like an overview of OpenCV basics, here is one).
Having said that, let’s establish some standards we’ll be following in this and subsequent entries:
import cv2 as cv
# assuming we:
# - loaded frames from cv2.VideoCapture into a `video` array
# - the video in question is 1080p, and in color
frame = cv.cvtColor(video[frame_index], cv.COLOR_BGR2RGB)
print(frame.shape) # (1080, 1920, 3)
print(frame.type) # dtype('uint8')
print(frame.max()) # 255In other "words", unless stated otherwise:
-
we’ll be using the RGB colorspace (after all, anyone using OpenCV for any length of time has an "amusing" story of accidentally using its BGR default);
-
our color values will be in the
0-255range.
Designating the designator
We’re now looking for distinguishing features of the target designator, so that we can use that information to extract it from the input videos' frames in later, upcoming blog entries.
| Fair warning about this section – we’ll be going pretty deep here, and sometimes into seemingly redundant paths. This is to show more possibilities than just the "optimal" solution for this particular case. |
Going back to the matter at hand – looking at the last screenshot again, it becomes pretty obvious the distinctive quality of the target designator is its color. In fact, let’s see a couple more examples of the designators:

We can observe a couple of things:
-
the boxes are:
-
of size 96px by 96px, at least in the input samples are using;
-
in general, very red,
-
they are, however, not uniformly red, due to blending at the borders, video encoding particularities, and a slight translucency applied throughout;
-
-
-
the target designators can be, themselves, obscured by other UI elements, like the ring (arm) and crosshair (torso) reticles,
-
they are also not the only elements that appear to have this particular color – in two of the examples, we can see a third kind of reticle for lock-on weapons (no one said this game isn’t complex!) that, in its active state, has visually the same hue.
Let’s see how distinguishable that color is among the various reticles. The first kind of visualization tool that may come to mind is a histogram. We’ll use the following functions to generate them:
import numpy as np
import pandas as pd
import seaborn as sns
PIXEL_VALUE_LIMITS = (0, 255)
def to_channel_values_in_rows(image):
channel_width = image.shape[-1]
return np.moveaxis(image, len(image.shape)-1, 0).reshape([channel_width, -1])
def histogram_from_image(image, plt_axis, labels, colors, max_samples):
channel_values_in_columns = np.transpose(to_channel_values_in_rows(image))
hist_data = pd.DataFrame(data=channel_values_in_columns, columns=labels)
sns.histplot(hist_data, ax=plt_axis, palette=colors, binwidth=10)
plt_axis.set_ylim(0, max_samples) # necessary for consistency across all imagesInstead of using matplotlib histograms, we’re going for seaborn’s version instead. This allows to more concisely define the graph parameters such as the colors and labels for each data element. We also need to extract the actual value frequencies from each color channel for the histogram to make sense – that’s where the to_channel_values_in_rows function comes in, converting the [y][x][channel] –> value mapping of the image into an array of dimension (channel_width, width*height), where every row lists the intensity values of pixels for the particular channels.
For an RGB histogram, we invoke the function like so:
histogram_from_image(image, axs_from_matplotlib, ["r", "g", "b"], ["r", "g", "b"], 96**2 * 0.5)The max_samples is derived from the size of the image (target designator size), but ultimately something obtained via trail-and-error.
OK, let’s see what we got:
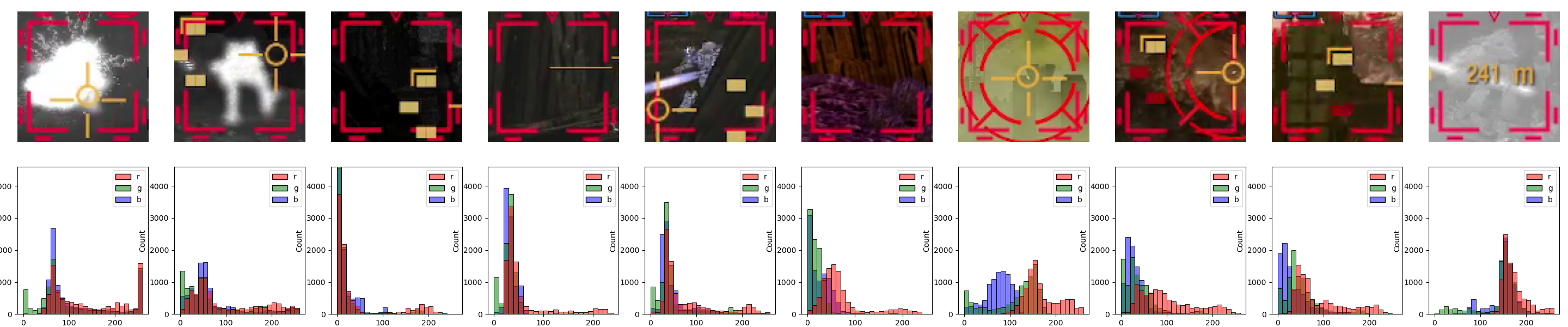
That’s not… very helpful, is it? The values are seemingly all over the place, we can mayyyybe make out a small bump in the R-channel’s values around 200, but that’s it.
We mustn’t give up on histograms quite yet, 'though. RGB is not the only colorspace. Alternatives include HSL and HSV colorspaces that, as the linked Wikipedia page states, align more closely with human visual perception than RGB.
Onto the histograms:
histogram_from_image(cv.cvtColor(image, cv.COLOR_RGB2HLS), axs_from_matplotlib, ["H", "L", "S"], ["black", "magenta", "cyan"], 96**2 * 0.5)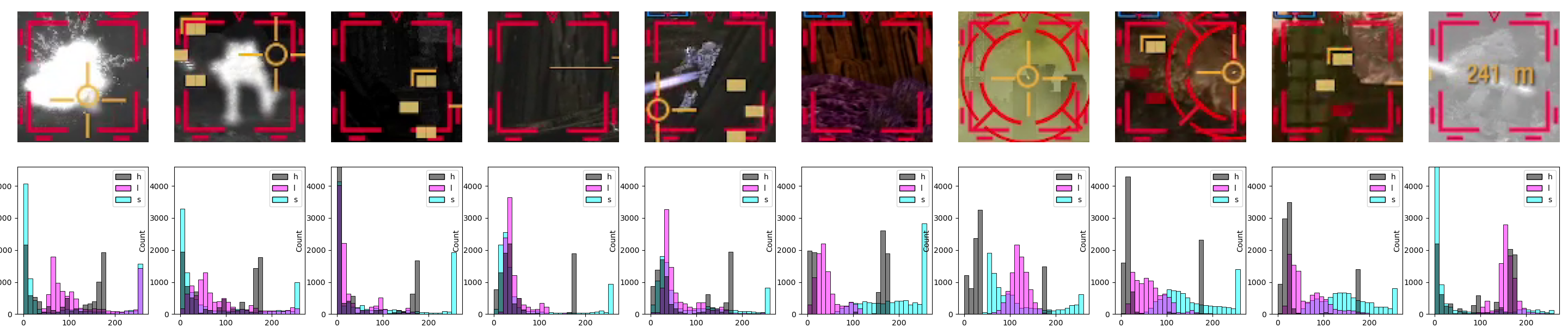
Immediately, we see that all diagrams have a distinctive peak in the Hue channel, within the 170-180 bin. So, what does, say, 175 at max saturation and half lightness (both for better color visibility) looks like? Like this:
SWATCH_IMAGE_SIZE = 40
COMPONENT_VALUE_MAX = PIXEL_VALUE_LIMITS[1] # 255 in our case
def display_color_swatch(h, l, s, image_size=SWATCH_IMAGE_SIZE):
demo_image = np.tile([h, l, s], (image_size, image_size, 1)).astype('uint8')
# housekeeping to ensure image is displayed in 1:1 ratio
figsize(image_size * px, image_size * px)
plt.axis('off')
plt.tight_layout(pad=0)
plt.imshow(cv.cvtColor(demo_image, cv.COLOR_HLS2RGB))
plt.show()
h = 175
s = COMPONENT_VALUE_MAX
l = COMPONENT_VALUE_MAX / 2
display_color_swatch(h, l, s)Yeah, that does look red all right.
| In the previous couple of snippets, we’ve been using HLS (instead of HSL) since that what OpenCV offers (similarly to BGR vs RGB). Keep that in mind, so as not to mix up the channels. |
For good measure, let’s take a portion of each of the boxes – in this case, the "upper-left" one, i.e. image[8:37, 7:10, :], and generate the histograms for that:
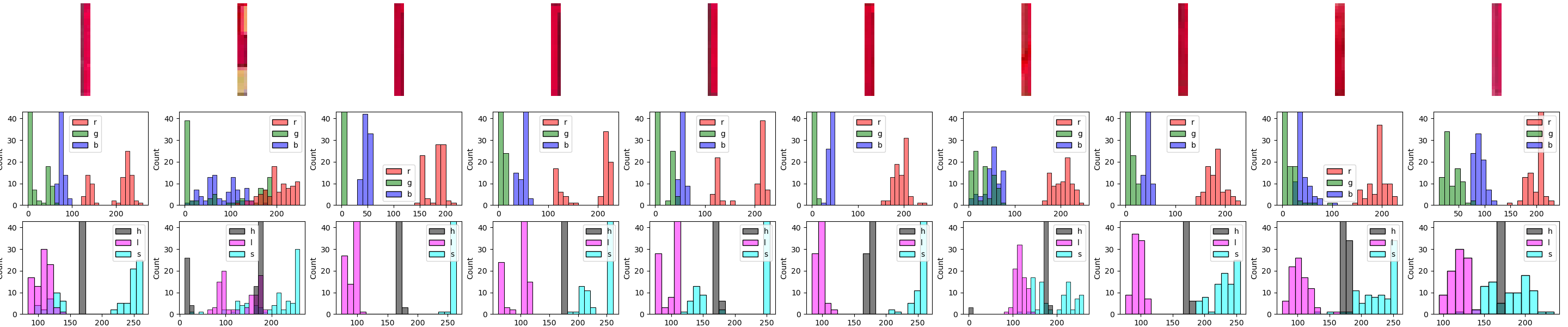
This indicates even more strongly that just going by hue value might be our ticket (since the same "spike" is visible right around the 170-180 bin).
To preempt the eventuality that masking by a single channel value might be insufficient, we can examine the relationship between the different channels. At first, visually. We need a 3D scatter plot. Our function to generate one looks like this:
AX3D_PREFIX_SETTER = "set_"
AX3D_AXES = ["x", "y", "z"]
AX3D_LIM_SUFFIX = "lim3d"
AX3D_LABEL_SUFFIX = "label"
def set_up_3d_plot_limits_and_labels(ax, labels: tuple[str, str, str]):
"""Helper function - sets all axes limits and labels"""
def __ax3d_funcs(ax3d, suffix):
return [getattr(ax3d, f"{AX3D_PREFIX_SETTER}{axis}{suffix}") for axis in AX3D_AXES]
for limit_setter in __ax3d_funcs(ax, AX3D_LIM_SUFFIX):
limit_setter(*PIXEL_VALUE_LIMITS)
for label_setter, label in zip(__ax3d_funcs(ax, AX3D_LABEL_SUFFIX), labels):
label_setter(label)
def scatter_3d_from_image(image, labels, fig, plt_axis, num_columns, num_rows, column, row):
channel_values_in_rows = to_channel_values_in_rows(image)
plt_axis.axis('off')
ax = fig.add_subplot(num_rows, num_columns, (row * num_columns) + column + 1, projection="3d")
set_up_3d_plot_limits_and_labels(ax, labels)
ax.scatter(*channel_values_in_rows)And our invocation, for example, for the 2nd row, and the 3rd image, might look like this:
fig, axs = plt.subplots(3, 10)
row = 1
image_index = 2
# Some code in between...
scatter_3d_from_image(frame, ["r", "g", "b"], fig, axs[1, 2], 10, 3, 2, 1)
The code for the current visualization appears convoluted. That’s because we’re mixing up 2D and 3D diagrams in one plot. The 3D elements force us to use the fig.add_subplot API, whereas our 2D elements are reliant on the plt.subplots API, with array of 2D axes. This is why we also include the plt_axis.axis('off') call – we need to "hide" the axes of the 2D diagram "slot" we’ve created with plt.subplots.
|
Right, let’s see our results:
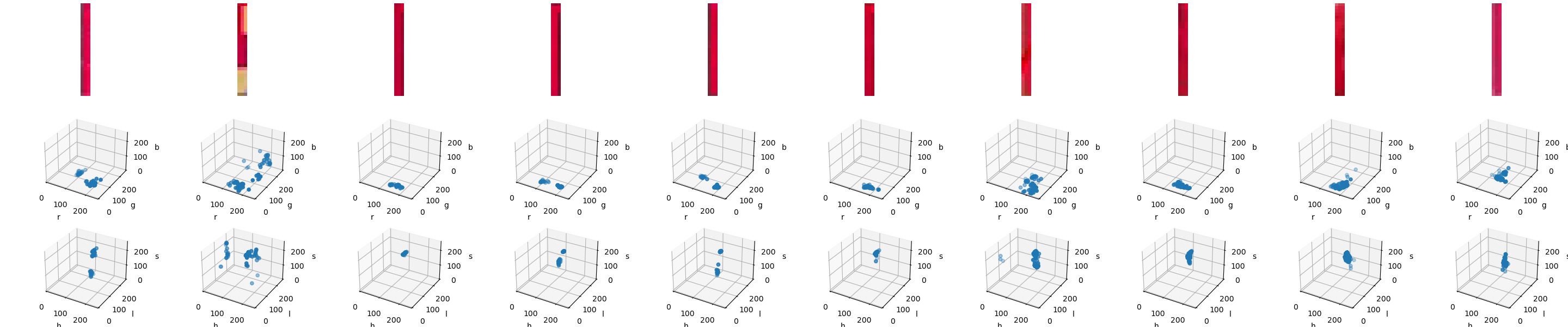
For the fragment version, the clustering across the two different colorspaces is pretty similar — arguably, the HLS one looks more "compact", but that might be misleading. The full designator versions offer a starker difference between RGB and HLS. In most cases, in the HLS plot, we can make out the same kind of cluster as in the fragment diagrams, whereas the RGB versions are much more of a chaotic jumble.
However, it is high time we started to act like true MechWarriors – in this case, stop relying on the MK. I Eyeball, and turn to cold and calculating machine systems for our target acquisition. This means, in our case, clustering.
What we’ll do now is join both imagesets into large images, and run a clustering algorithm on them. This will "smoothen out" differences across our samples and hopefully make the cluster we’re interested in - the target designator color cluster – more pronounced, and thus easier to pick out by the algo.
Speaking of algos, scikit-learn has a very convenient overview of the clustering algorithms it offers. Now, we need to consider our requirements and preferences.
As far as requirements are concerned, anything with "even cluster sizes" is right out. Not only it’s unlikely to be the case just looking at the variability of colorspace values across our images, but also we’re really interested in the one (postulated) cluster that will represent the target designator colorspace values. So K-Means, Spectral clustering and Bisecting K-Means should be excluded.
For scaling, we don’t really about it – our data space size is too small for it matter significantly.
We now have a choice of two broad categories of algos, split on the kind of main parameter, that being:
-
distance threshold: this is… kind of what we want to obtain from the clustering. We can have a good guess, but let’s maybe leave algos requiring in case something doesn’t work.
-
neighborhood size: also arguably something that we want to get from the clustering, but in this case we can at least estimate some minima from the size of the box elements. So, let’s go with that first.
This leaves us with Affinity propagation, DBSCAN, OPTICS, Gaussian mixtures, and BIRCH. We can start with any one of them. However, DBSCAN looks like the best candidate so far. That’s because of a quirk in its parametrization. To quote the docs:
[…] the parameter eps is crucial to choose appropriately for the data set and distance function and usually cannot be left at the default value. It controls the local neighborhood of the points. When chosen too small, most data will not be clustered at all (and labeled as -1 for “noise”).
This low amount of clustering and labeling most data as "noise" is, in our case, exactly what we want!
Let’s get to work then. First, let’s merge all our images into one – we can do this with a NumPy array-level operation:
# all images
designator_images: list[np.array] = ...
# all with just the designator segments
designator_segment_images = [img[8:37, 7:10, :] for img in designator_images]
designator_image_concat = np.concatenate(designator_images, axis=1)
designator_segment_images_concat = np.concatenate(designator_segment_images, axis=1)This will produce the following two images:


Let’s start with the latter first, as the result obtained from that will help us find the "right" cluster of interest in the former. In fact, because this image contains just (a portion) of the designator, we want the clustering algorithm to generate exactly 1 cluster, and leave the rest as noise.
Alright, so DBSCAN has several parameters, of which two are of particular interest: eps and min_samples. Both determine how the neighborhood of "core" points is defined – an important distinction, by the way, between that and the size of the entire cluster, which DBSCAN does not concern itself with directly.
Keeping this sizing caveat in mind, we’ll ballpark both parameters.
For eps, we want a decent, but not to overly broad of a distance, so that the cluster doesn’t capture too many points. A good value would be to at least allow a distance of 2 in any direction (H, S, L). Since we’re keeping the default Euclidean metric, this gives us eps=2**3=8. Of course, this also lets through points that are 8 values away along any one axis, but this won’t be a problem here.
Now, min_samples. One would be tempted to get a large number, like the size of a single of one of the 3 "bars" each designator segment has (recall the individual images are of shape (3, 28) in this case). This would give us 28*10=280 (10 being the image count). Great! Except it won’t work – no cluster will be recognized. No "core" point can apparently be found for the given eps value in this case. However, half of that, i.e. 140 works, so let go with that.
Our clustering result is generated through the following code:
from sklearn.cluster import DBSCAN
def prepare_image_for_clustering(image):
# since we've determined HSL/HLS to likely be superior for clustering
hsl = cv.cvtColor(image, cv.COLOR_RGB2HLS)
# DBSCAN, as typical of sklearn Estimators, needs a columnar format of the values
in_rows = to_channel_values_in_rows(hsl)
return np.transpose(in_rows)
def hsl_clusters_of(X, eps, min_samples):
# we're explicitly adding that we want a l2/Euclidean metric
dbscan = DBSCAN(eps=eps, min_samples=min_samples, p=2)
# our clustering fit
return dbscan.fit_predict(X)
X_segment = prepare_image_for_clustering(designator_segment_images_concat)
clusters = hsl_clusters_of(X_segment, eps=2 ** 3, min_samples=(28 * 10) // 2)clusters is simply a 1-D denoting which cluster a given sample belongs to. We’ll fit it into a dataframe to allow for analysis and display[1] :
COLORSPACE = ("H", "L", "S")
def cluster_to_df(image_data_h_l_s, clusters):
return pd.DataFrame(data=zip(image_data_h_l_s[:, 0], image_data_h_l_s[:, 1], image_data_h_l_s[:, 2], clusters), columns=list(COLORSPACE)+["cluster_id"])
clustering_df = cluster_to_df(X_segment, clusters)and start verifying that we got our desired result:
clustering_df["cluster_id"].value_counts()
# prints out:
# -1 480
# 0 390
# Name: cluster_id, dtype: int64Yup, we’ve got our single cluster (since -1 is the special "noise" value). Now for the cluster’s summary statistics:
target_values = clustering_df[clustering_df["cluster_id"] == 0]
target_values.describe()
# prints out:
# H L S cluster_id
# count 390.000000 390.000000 390.000000 390.0
# mean 172.815385 101.858974 254.423077 0.0
# std 1.672942 8.157392 1.863733 0.0
# min 170.000000 83.000000 243.000000 0.0
# 25% 172.000000 96.000000 255.000000 0.0
# 50% 173.000000 102.000000 255.000000 0.0
# 75% 174.000000 109.000000 255.000000 0.0
# max 179.000000 121.000000 255.000000 0.0The mean hue value is close to what we estimated earlier from the histograms.
Now, let’s try to run the clustering on the concatenated full designator images. We’re going to multiply min_samples by 4, as every image has that number of previously extracted segments.
X_designators = prepare_image_for_clustering(designator_image_concat)
clusters_full = hsl_clusters_of(X_designators, eps=2 ** 3, min_samples=((28 * 10) // 2)*4)
clustering_df_full = cluster_to_df(X_designators, clusters_full)
clustering_df_full["cluster_id"].value_counts()
# prints out:
# -1 61136
# 1 7300
# 2 4137
# 5 3869
# 7 3185
# 4 2553
# 3 2082
# 9 1989
# 6 1886
# 0 1795
# 8 1597
# 10 631Lots more clusters, but that’s to be expected. The first cluster is hopefully want we want, followed by, most likely, greyscale values in some of the test images. Not leaving anything to chance, let’s check out what hue values are represented by each cluster.
We’re going to calculate three percentiles of the hue values for each cluster: the 10th, the 50th (i.e., median), and the 90th. This is a serviceable exploration heuristic if a quick check is desired, and a relatively varied distribution is suspected. We’re also including the cluster size again, for good measure.
from functools import partial
# The keywords of agg are completely arbitrary - they're just
# our column names in the output. What is important is that we provide
# a function object (Callable) for each value. That is why we need to
# invoke partial for the percentiles.
clustering_df_full.groupby(by="cluster_id")["H"].agg(centile_10=partial(np.percentile, q=10),
median=np.median,
centile_90=partial(np.percentile, q=90),
count=len)
# prints out:
# centile_10 median centile_90 count
# cluster_id
# -1 7.0 30.0 173.0 61136
# 0 0.0 0.0 0.0 1795
# 1 171.0 173.0 177.0 7300
# 2 0.0 0.0 0.0 4137
# 3 0.0 5.0 13.0 2082
# 4 30.0 30.0 30.0 2553
# 5 15.0 26.0 34.0 3869
# 6 7.0 16.0 20.0 1886
# 7 27.0 31.0 33.0 3185
# 8 165.0 165.0 168.0 1597
# 9 0.0 0.0 0.0 1989
# 10 0.0 0.0 0.0 631(by the way: yes, we could have just used describe here – the only benefit is a slightly more focused output. Don’t worry, we’ll come back to that method later on.)
Phew, looks like we do have most of the relevant values in one cluster (cluster_id == 1). The guess that the other of the largest clusters represent greyscale values was also correct (if you’re wondering why there are multiple ones with H values 0 – that’s because they almost certainly differ in the other colorspace components).
The only mildly worrying thing is cluster 8, being very close in hue to the red of our designator. We’ll keep that in mind as we progress into the next steps.
Before we close this section, it would serve us to actually visualize the cluster spaces. We’re going to do it in two ways – one, by using a predefined colormap, the other, by using the actual (median) colors of the cluster. The code for the diagram generation is as follows (warning – lots of matplotlib idiosyncrasies we won’t go into detail here):
import matplotlib.patches as mpatches
MISSING_CLUSTER_ID = -1
MISSING_CLUSTER_COLOR = [0.75, 0, 0.75]
LEGEND_VALUES_PER_COL_MAX = 2
def show_legend_no_alpha(ax, colors, labels, title):
"""Helper function - displays a legend for the cluster colors with 0 transparency"""
# removing the alpha channel (RGBA -> RGB)
handles_colors = [c[:3] for c in colors]
# following
# https://matplotlib.org/stable/tutorials/intermediate/legend_guide.html#creating-artists-specifically-for-adding-to-the-legend-aka-proxy-artists
final_handles = [mpatches.Patch(color=color, label=label) for (color, label) in zip(handles_colors, labels)]
# and ensure that the cluster values are the labels...
ax.legend(handles=final_handles, ncols=(len(final_handles) // LEGEND_VALUES_PER_COL_MAX) + 1, loc="upper right", title=title)
def draw_clusters_cm(cluster_data: pd.DataFrame, alpha: float = 1., colormap="tab20b"):
"""Primary presentation function – draws provided clusters with a predefined colormap
See https://matplotlib.org/stable/tutorials/colors/colormaps.html
"""
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
set_up_3d_plot_limits_and_labels(ax, COLORSPACE)
scatter_plot = ax.scatter(*[cluster_data[comp] for comp in COLORSPACE],
c=cluster_data["cluster_id"],
alpha=alpha,
cmap=colormap)
handles, labels = scatter_plot.legend_elements()
show_legend_no_alpha(ax, [c.get_color() for c in handles], labels, "cluster_id")
plt.show()
def draw_clusters_real_color(cluster_data: pd.DataFrame, alpha: float = 1.):
"""Alternative presentation function – draws provided clusters with "real" colors,
i.e. each of the median HLS values for the cluster."""
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
set_up_3d_plot_limits_and_labels(ax, COLORSPACE)
# create a color dict for the cluster colors
median_cluster_colors = cluster_data.groupby("cluster_id")[list(COLORSPACE)].median()
median_cluster_color_rgb = cv.cvtColor(np.array([median_cluster_colors.values]).astype('uint8'), cv.COLOR_HLS2RGB)
colors_per_cluster = dict(
list(zip(median_cluster_colors.index,
(median_cluster_color_rgb[0] / float(PIXEL_VALUE_LIMITS[1])).tolist())))
# let's set -1 to an unusual color, but background color (such as light magenta) for good measure
if MISSING_CLUSTER_ID in colors_per_cluster:
colors_per_cluster[MISSING_CLUSTER_ID] = MISSING_CLUSTER_COLOR
# we're doing things differently now - drawing individual scatter plots per cluster
for cluster_id, color in colors_per_cluster.items():
cluster_data_specific = cluster_data[cluster_data["cluster_id"] == cluster_id]
ax.scatter(*[cluster_data_specific[comp] for comp in COLORSPACE],
color=color,
label=cluster_id,
alpha=alpha,
)
handles, labels = ax.get_legend_handles_labels()
show_legend_no_alpha(ax, [h.get_edgecolor()[0] for h in handles], labels, "cluster_id")
plt.show()and these are the diagrams we want to generate:
draw_clusters_real_color(clustering_df[clustering_df["cluster_id"] == 0])
draw_clusters_cm(clustering_df_full[clustering_df_full["cluster_id"] != -1])
draw_clusters_real_color(clustering_df_full[clustering_df_full["cluster_id"] != -1])
draw_clusters_real_color(clustering_df_full, 0.01)which gives us the following:
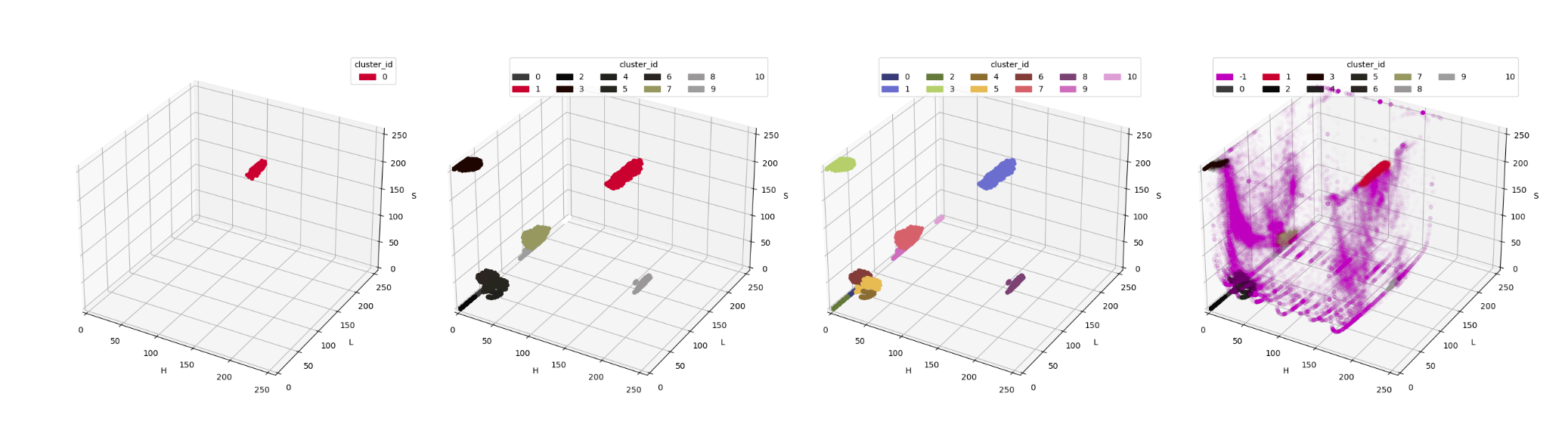
Couple of notes here:
-
we were needlessly concerned about cluster
8being, perhaps, cluster1's "lost twin" – from the diagram, especially the median color diagram, it is apparent that this cluster is actually very far away in our colorspace. Just shows the importance of properly presenting data and information extracted therefrom, and not jumping into conclusion based on solely a partial view of the data. -
speaking of visualisation:
-
compare diagram 2 with diagram 3 – while the "true color" diagram provides some immediate information as to what the clusters represent, only the "palette" really demonstrates cluster boundaries.
-
for the final diagram, the alpha of all points is reduced greatly. This is because the no-cluster classification dominates within our dataset, so using no alpha would render our diagram pretty much unreadable.
-
And now, for the pièce de résistance – color information for cluster 1 in the full image!
Or, well, it would be, but we need to take of one thing first. Some readers have probably noticed the way we calculated the median color values of the cluster, i.e., get the median of each individual HSL component. That grouping of values is actually a marginal median. It is not the sole representation of a median in multidimensional spaces. In fact, depending on your dataset and on the relations between the components, it may be completely non-representative of the examined data, as discussed in this answer on Cross Validated.
At the surface level, the Cluster Of Interest looks like your typical unassuming, convex blob with likely straightforward relationships between the components. This may be deceiving, as, just by looking at the diagram, we cannot really see what the actual value densities are within that cluster. So, let’s go one step further and make sure we get our values right.
Another, somewhat more generally robust median in a multidimensional space is the geometric median[2]. It’s not available out-of-the-box in Pandas or numpy – but there is a third-party library that provides it.
To calculate it, we first need to extract the combined HLS values into a dedicated column:
# filtering out just the cluster of interest
cluster_1_data = clustering_df_full[clustering_df_full["cluster_id"] == 1].drop(columns=['cluster_id'])
# extracting the combined values
cluster_1_data["HLS"] = [r for r in cluster_1_data[["H", "L", "S"]].values]
# normalizing them to [0,1], as needed for the median calculation
# doing so in a separate step means we have access to the vectorized operation syntax
cluster_1_data["HLS_norm"] = cluster_1_data["HLS"]/COMPONENT_VALUE_MAX
# keeping just the normalized combined column
cluster_1_data = cluster_1_data.drop(columns=["HLS"])Now we can actually obtain the geometric median:
from geom_median.numpy import compute_geometric_median
def compute_geom_median_on_series(series: pd.Series):
result = compute_geometric_median(series.values)
# "denormalize" the result back to [0, 255]
return result.median*COMPONENT_VALUE_MAX
geometric_median = cluster_1_data["HLS_norm"].agg(compute_geom_median_on_series)
geometric_median
# prints out
# array([173.03971593, 100.6201285 , 254.43690908])Now to demonstrate it, using the color swatch function we’ve defined previously…
# "unwinding" the result array into positional arguments
# important to keep the sequence right, which in this case
# it is (H,L,S)
display_color_swatch(*geometric_median)…and compare to the individual medians:
color_components = ["H", "L", "S"]
cluster_1_data[color_components].agg(np.median)
# prints out
# H 173.0
# L 101.0
# S 255.0
# dtype: float64We can see that, while in this case, the result is almost identical, there is still a small difference (in the saturation).
For good measure, let’s also generate more summary statistics for the color components, this time using describe:
color_components = ["H", "L", "S"]
cluster_1_stats = cluster_1_data[color_components].describe(percentiles=[0.1, 0.5, 0.9]).round(2)
cluster_1_stats
# prints out
# H L S
# count 7300.00 7300.00 7300.00
# mean 173.59 96.76 253.86
# std 2.39 15.72 3.06
# min 168.00 55.00 240.00
# 10% 171.00 72.00 250.00
# 50% 173.00 101.00 255.00
# 90% 177.00 114.00 255.00
# max 180.00 127.00 255.00Finally, let’s summarize our results into a single DataFrame:
cluster_1_stats_final = cluster_1_stats.copy()
cluster_1_stats_final.loc["geom_median"] = geometric_median
cluster_1_stats_final = cluster_1_stats_final.drop(index=["count"]).round(2)
cluster_1_stats_final
# prints out
# H L S
# mean 173.59 96.76 253.86
# std 2.39 15.72 3.06
# min 168.00 55.00 240.00
# 10% 171.00 72.00 250.00
# 50% 173.00 101.00 255.00
# 90% 177.00 114.00 255.00
# max 180.00 127.00 255.00
# geom_median 173.04 100.62 254.44Summary
The numerical values we’ve now obtained will help us gauge the extent of the filtering criteria, as we move on to actually extracting the designators themselves.
Now, was this much work necessary to determine the colors that interest us? The answer is "absolutely not".
We could’ve just put the example images into an image editor and let it sample the color. Then, we might’ve eyeballed the color component intervals (i.e., min, max, and so on) for the purpose of creating a prototype extractor of the designator images. This is, in fact, the level of effort that should usually be applied when making prototypes.
Hell, we could’ve gone with an alternative route (if allowed by relevant copyright law and additional agreements such as the EULA) – look into the game’s graphic assets, if available, and find the elements from which the designator is constructed. This would allow us to estimate the color range from stuff like the designator’s alpha channel[3].
Moreover, our data size is suspiciously small. In a project of similar magnitude, we should have hundreds, if not thousands of samples to use for the clustering. The reliability of the result rests pretty much on the author’s confidence to handpick representative samples consistently.
The intent of this post, however, was twofold.
First, to demonstrate how to go about solving this kind of problem somewhat more rigorously, so that we can have a little bit more confidence in what we base our further work on.
The other was showcasing a number of data analysis tools and the way to use them, allowing them to be used when tackling similar data extraction tasks.
Well, here we are. In the next couple of entries, we’ll proceed with the image extraction itself, using several different techniques of varying complexity, power, and performance. To provide a bit of a teaser: in the immediately subsequent post, we’ll start with a couple of simple and current techniques, including the usage of some libraries that are definitely more modern than OpenCV. Watch this space!


Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Email